Statistical Modeling & Regression Predicting The Future

Introduction (Statistical Modeling & Regression)

Everyday Predictions You Already Trust

Have you ever stopped to think about how many of your daily decisions are quietly shaped by numbers? Not numbers you consciously calculate, but predictions generated for you in the background.

Take weather apps, for example.

You wake up, unlock your phone, and see a neat little forecast: “80% chance of rain this afternoon.” Without a second thought, you toss an umbrella into your bag before heading out. Hours later, as the skies darken and raindrops fall, you feel a quiet satisfaction. The app didn’t just guess it knew. To you, it feels like magic. But behind that simple percentage is a powerful mathematical framework at work statistical modeling.

Entertainment That Reads Your Mind

Now imagine a different scene. After a long day, you plop onto your couch, open Netflix, and suddenly your screen is filled with recommendations. Some shows you’ve never heard of, yet they seem almost custom-picked for your taste. You take the bait, click on one, and find yourself binging episode after episode.

You wonder: “How does Netflix always know what I want to watch before I even know it myself?” The truth isn’t witchcraft or mind-reading. It’s data. Every choice you’ve made — every pause, every skipped episode, every five-star rating — feeds into complex regression models that study patterns in your behavior and compare them to millions of other users. Out of that chaos of numbers emerges order: a curated list that feels personal, even intimate.

Business Decisions Powered by Data

Let’s shift to the business world. A small retail store is preparing for the holiday season. Instead of relying on gut feeling or guesswork, the manager studies last year’s sales, looks at trends, considers variables like weather, promotions, and customer demographics. Using regression analysis, she builds a model that predicts which products are likely to sell fast and which might gather dust on the shelves.

She acts on the insights:

increases orders for trending products, reduces stock for low-demand ones, and tailors marketing campaigns to the right customers. The result? Higher profits, lower waste, and customers who feel like the store always has exactly what they want.

Here again, the difference between a thriving season and a financial flop comes down to the same tool statistical modeling and regression.

The Hidden Hero (Regression Analysis)

From weather apps to streaming platforms, from small businesses to global corporations what ties all these scenarios together? The unsung hero called regression analysis.

Regression isn’t just math for statisticians, it’s a universal translator that turns raw, messy data into meaningful stories. It helps us answer questions like:

• Does spending more on marketing really increase sales?
• How does age, diet, and exercise influence health outcomes?
• What variables most strongly affect house prices in a city?

By identifying patterns and relationships among variables, regression allows us to peek into the future with surprising accuracy. It gives shape to uncertainty, transforming random noise into reliable predictions.

Why This Article Matters

Here’s the truth: regression models are everywhere, quietly shaping decisions that affect our lives. Yet, for many, the words “statistical modeling” still feel abstract, intimidating or irrelevant.

This article aims to break that wall. We’ll peel back the complexity and show you not only what statistical modeling and regression are, but also why they matter so much in the modern world. From simple examples to advanced applications, you’ll see regression as more than just equations. You’ll see it as a decision-making superpower one that powers businesses, governments, and the technology you use every single day.

So, whether you’re a student dipping your toes into statistics, a professional seeking to make smarter data-driven choices, or simply a curious reader, this journey will help you understand why regression truly is the hidden hero of our data-driven age.

What is Statistical Modeling?

A Simple Definition

At its core, statistical modeling is the process of creating a simplified mathematical representation of reality. In other words, we take messy, real-world data sales figures, temperatures, customer ratings, health records and build a model (a kind of equation or structure) that explains patterns and relationships in that data.

Think of it like making a map. A map is not the territory itself; it’s a simplified version that highlights the most important features roads, landmarks, distances. Similarly, a statistical model doesn’t capture every tiny detail of reality. Instead, it captures the key relationships between variables that help us understand and predict outcomes.

Formally, a statistical model is a mathematical function that describes how one or more independent variables (inputs) affect a dependent variable (output).

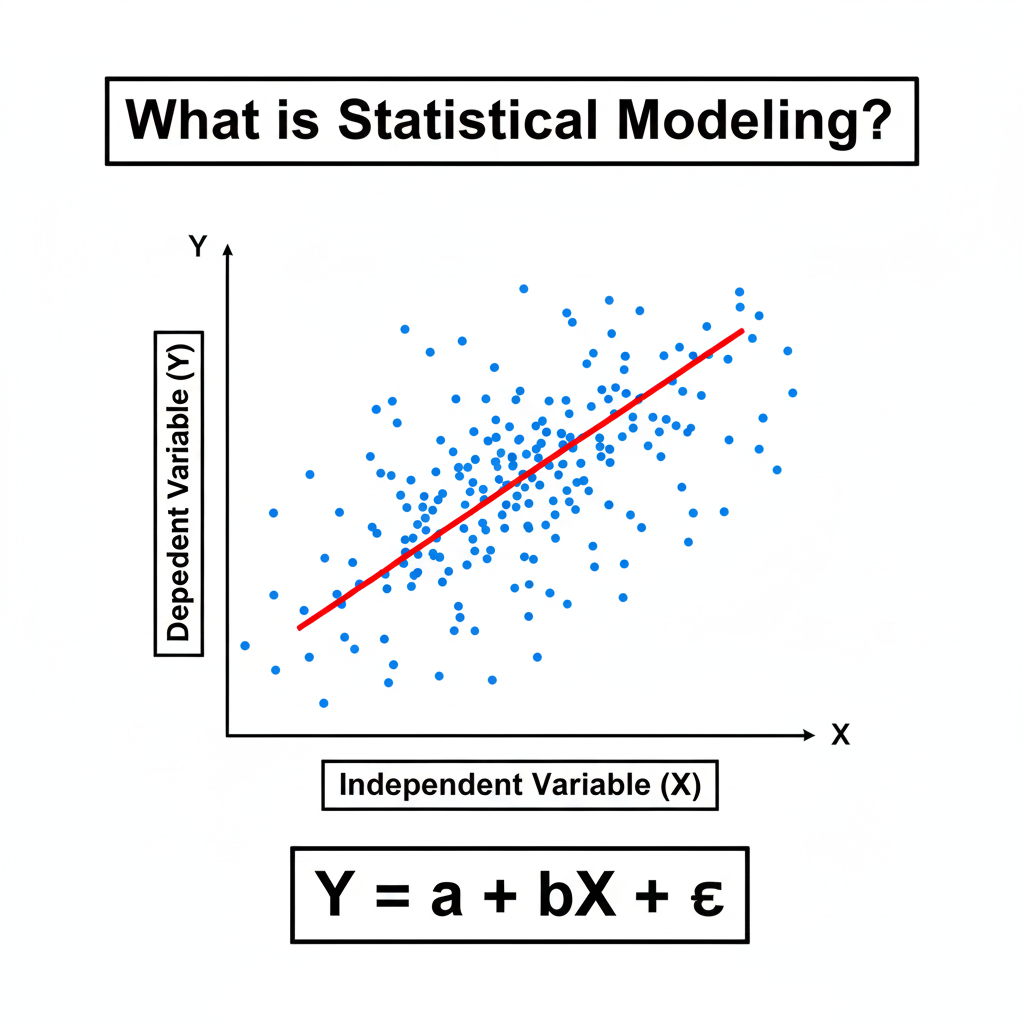
The general form looks like this:

Y=f(X)+ϵ

• Y = Dependent variable (the outcome we want to predict, e.g., sales, temperature).
• X = Independent variable(s) (factors that influence the outcome, e.g., advertising spend, time of year).
• f(X) = The function (our model) that describes the relationship between X and Y.
• ϵ = Error term (the randomness or noise that the model cannot explain).

Why We Need Models in the First Place

The world is full of uncertainty. Data on its own is overwhelming thousands of numbers in a spreadsheet don’t automatically tell us anything useful. What we need is a way to find structure in that chaos.

That’s where models come in.

• They help us understand relationships. (e.g., Does more exercise really reduce heart disease risk?)
• They allow us to predict future outcomes. (e.g., How many customers will buy next month if we spend $10,000 on ads?)
• They support decision-making. (e.g., Should a bank approve this loan application based on income and credit history?)

Without models, we did not be guessing. With them, we base decisions on patterns backed by data.

Everyday Analogies

Weather Forecasting

Meteorologists don’t guess the weather. They build statistical models that combine temperature, humidity, pressure, and wind speed to predict tomorrow’s weather. A simplified version might look like:

Temperaturetomorrow​=a+b1​(Humidity)+b2​(Pressure)+b3​(WindSpeed)+ϵ

House Prices

Realtors often predict house prices based on square footage, number of bedrooms, and neighborhood.

Price=a+b1​(Size)+b2​(Bedrooms)+b3​(Location)+ϵ

Here, each coefficient (b1, b2, b3b​) tells us how much that factor contributes to the overall price.

Health Outcomes

Doctors may use models to predict a patient’s risk of developing diabetes based on factors like age, weight, and family history.

Risk=a+b1​(Age)+b2​(BMI)+b3​(Genetics)+ϵ

Why It Matters

Statistical modeling is more than math it’s about turning data into actionable insight. Instead of drowning in numbers, we build a lens through which patterns become visible. With a good model, businesses make smarter investments, governments design better policies, and individuals make better personal choices.

In short: a model is a story told with data.

Regression Analysis (The Backbone of Modeling)

What Does “Regression” Really Mean?

At first, the word regression might sound technical, maybe even intimidating. But at its heart, regression simply means:

👉 Finding the relationship between variables so that we can understand the past and predict the future.

Think of regression as drawing a line (or curve) through a cloud of data points on a graph. That line represents the best possible explanation of how one thing affects another.

For example:

• Does the number of study hours affect exam scores?
• Does marketing budget influence sales?
• Does temperature impact electricity usage?

Regression gives us a mathematical way to answer these questions.

The simplest form of regression looks like this:

Y=a+bX+ϵ

Where:

• Y = dependent variable (the outcome we want to predict, e.g., sales).
• X = independent variable (the factor influencing the outcome, e.g., ad spend).
• a = intercept (value of Y when X=0).
• b = slope (how much Y changes when X increases by 1).
• ϵ = error term (random noise the model can’t explain).

In plain words: regression builds an equation that explains how changes in X are connected to changes in Y.

Why Is Regression So Widely Used?

Regression is one of the most widely used tools in statistics, economics, business, and data science and for good reason. It’s powerful, flexible, and surprisingly intuitive once you strip away the jargon.

Here’s why it’s everywhere:

1. Simplicity : At its core, regression is easy to interpret. A slope of 2 simply means: for every 1 unit increase in X, Y goes up by 2.
2. Prediction Power : Regression models aren’t just about understanding the past; they help forecast the future. Businesses, governments, and apps use it to make data-driven predictions.
3. Versatility : Whether it’s economics, healthcare, sports, or AI, regression adapts. From predicting house prices to diagnosing diseases, regression can model relationships in countless scenarios.
4. Foundation of Machine Learning : Many advanced machine learning algorithms are extensions of regression. Understanding regression means you’re already halfway into understanding predictive AI.

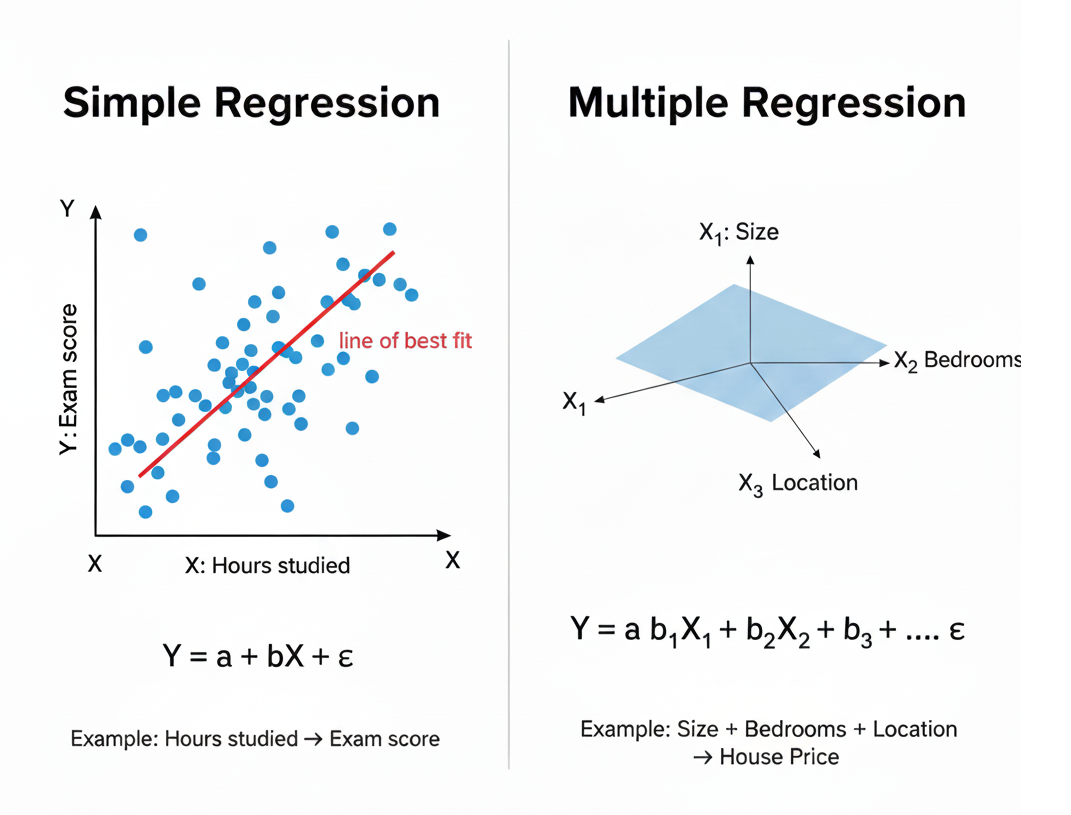
Simple Regression vs. Multiple Regression

1. Simple Linear Regression

This is the most basic form, where we look at the relationship between one independent variable (X) and one dependent variable (Y).

Formula:

Y=a+bX+ϵ

Example:
A student wants to know how study hours affect exam scores.

• Y = exam score.
• X = hours studied.
• b = how much the score improves per additional hour studied.

If the model says:

Score=40+5×(Hours)

It means: even if you study 0 hours, you’d score 40. Each extra hour of study adds 5 points to your exam score.

2. Multiple Regression

Real life is rarely influenced by just one factor. Multiple regression lets us study how several variables together affect an outcome.

Formula:

Y=a+b1X1+b2X2+b3X3+⋯+ϵ

Example:

Predicting house prices:

• Y = house price.
• X1​ = size (square feet).
• X2​ = number of bedrooms.
• X3​ = location score.

A model might look like:

Price=50,000+200(Size)+10,000(Bedrooms)+30,000(Location)+ϵ

Interpretation:

• For every extra square foot, the price increases by $200.
• Each bedroom adds $10,000.
• Being in a premium neighborhood adds $30,000.

This gives homeowners, buyers, and real estate agents a powerful way to estimate fair values.

The Big Picture

Regression analysis is the backbone of statistical modeling because it balances simplicity with explanatory power. With just a few variables and coefficients, we can uncover hidden patterns, quantify relationships, and make decisions that are grounded in data rather than guesswork.

In short: regression takes us from intuition to evidence, and from evidence to prediction.

Types of Regression Models

Regression isn’t one single technique it’s a family of approaches. Depending on the kind of data you have and the type of question you’re asking, different regression models step in. Let’s explore the most important ones.

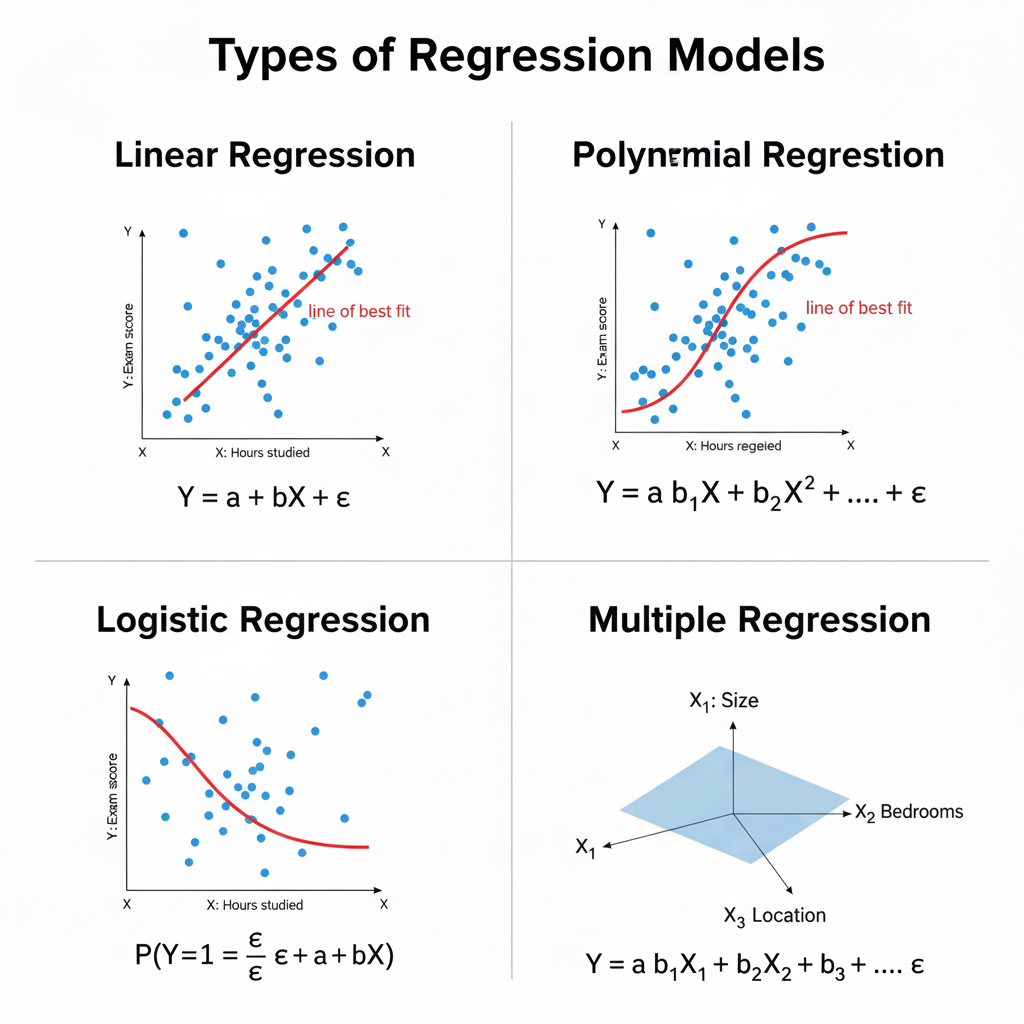
1. Linear Regression: Drawing the Straight Line

The simplest and most common type of regression is linear regression. As the name suggests, it assumes a straight-line relationship between the independent variable(s) and the dependent variable.

Formula:

Y=a+bX+ϵ

Where:

• Y = predicted outcome,
• X = independent variable,
• a = intercept,
• b = slope (rate of change),
• ϵ = error.

Example:
Suppose a student wants to know how much studying improves exam scores.

Score=40+5×(Hours)

Here, each hour of study adds 5 points to the exam score.

Real-World Use Case:

• Predicting salaries based on years of experience.
• Estimating crop yield based on rainfall.
• Forecasting demand for products based on advertising spend.

2. Multiple Regression (When One Factor Isn’t Enough)

Real life is rarely simple. Outcomes are often influenced by several factors at once that’s where multiple regression comes in.

Formula:

Y=a+b1X1+b2X2+b3X3+⋯+ϵ

Example:
A real estate agent wants to predict house prices based on three variables: size (sq ft), number of bedrooms, and neighborhood score.

Price=50,000+200(Size)+10,000(Bedrooms)+30,000(Location)

Real-World Use Case:

• Predicting house prices.
• Determining the impact of multiple marketing channels (TV ads, social media, billboards) on sales.
• Analyzing patient health outcomes based on diet, exercise, and medical history.

3. Logistic Regression: Predicting Yes or No

Not every outcome is a number. Sometimes, the question is binary: Will the customer buy or not? Will the patient recover or not? Is this email spam or not?

That’s where logistic regression shines. Instead of predicting a continuous value, it predicts the probability of an event occurring (between 0 and 1).

Formula (sigmoid function):

P(Y=1)=11+e−(a+bX)

Example:
A bank wants to predict whether a loan applicant will default (1 = default, 0 = no default). Logistic regression uses factors like income, credit score, and debt-to-income ratio to calculate the probability of default.

Real-World Use Case:

• Classifying emails as spam or not spam.
• Predicting customer churn (will a customer leave or stay?).
• Medical diagnosis (does the patient have the disease: yes or no?).

4. Polynomial Regression (When Life Isn’t a Straight Line)

Sometimes the relationship between variables is not linear. Think about the trajectory of a ball — it curves, it doesn’t move in a straight line. Polynomial regression allows us to model such curves by adding higher powers of XXX.

Formula:

Y=a+b1X+b2X2+b3X3+⋯+ϵ

Example:
A car company wants to study the relationship between speed and fuel efficiency. The graph shows a curve fuel efficiency improves at moderate speeds but drops sharply at very high speeds. Polynomial regression captures that U-shaped curve.

Real-World Use Case:

• Modeling growth rates in biology.
• Predicting sales that peak at certain times (like holiday seasons).
• Physics (motion of objects, trajectories).

5. Ridge Regression (Tackling Multicollinearity)

When multiple independent variables are highly correlated with each other, traditional regression may give unstable results. Ridge regression solves this by adding a “penalty term” to the equation, preventing coefficients from becoming too large.

Formula:

Minimize ∑(Y−Y^)2+λ∑bi2​

Here, λ is a penalty parameter that shrinks coefficients but never makes them zero.

Real-World Use Case:

• Predicting sales when advertising channels (TV, online, print) are correlated.
• Financial modeling when economic indicators overlap.
• Genetics research with thousands of correlated predictors.

6. Lasso Regression (Sparsity and Feature Selection)

Like Ridge, Lasso regression also adds a penalty, but this time it can shrink some coefficients all the way to zero. That means Lasso not only reduces overfitting but also performs automatic feature selection keeping only the most important predictors.

Formula:

Minimize ∑(Y−Y^)2+λ∑∣bi​∣

Real-World Use Case:

• Building models with many variables and automatically selecting the most important ones.
• Stock market analysis with hundreds of indicators.
• Text classification (selecting key words that matter most).

7. Advanced Methods: Beyond the Basics

Beyond Ridge and Lasso, modern data science uses hybrid and advanced regression techniques:

• Elastic Net Regression : Combines Ridge and Lasso for the best of both worlds.
• Quantile Regression : Useful when we care about predicting medians or percentiles instead of averages.
• Robust Regression : Helps when data has many outliers.

These methods are widely used in machine learning, where regression often forms the building blocks of algorithms for recommendation engines, fraud detection, and predictive analytics.

The Bigger Picture

Regression models may look like equations on paper, but in reality, they’re decision-making engines. From predicting your next favorite Netflix show, to forecasting company profits, to identifying whether a tumor is malignant or benign — regression quietly powers the insights behind some of the most important decisions in modern life.

In short: whether it’s a straight line (linear regression), a curve (polynomial), a yes/no prediction (logistic), or a high-dimensional machine learning problem (Ridge/Lasso), there’s always a regression model ready to turn raw data into actionable knowledge.

How to Build a Regression Model (Step-by-Step Guide)

Building a regression model isn’t just about throwing numbers into a computer and waiting for magic. It’s a systematic process like baking a cake. If you skip steps or add the wrong ingredients, the final result won’t turn out well. Let’s walk through the essential stages.

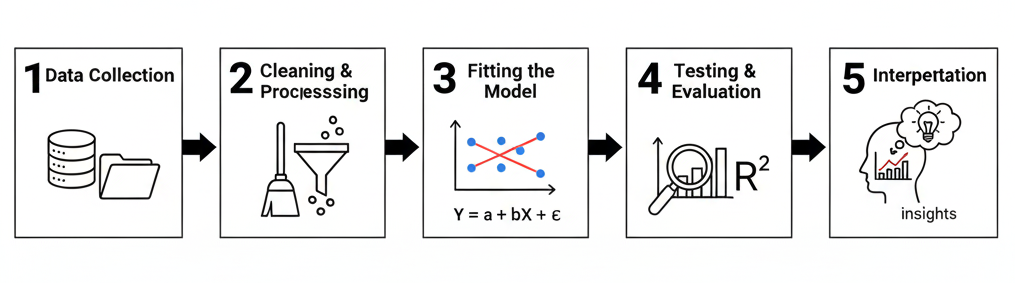
1. Data Collection (Gathering the Raw Ingredients)

Every model begins with data. Just as a chef needs fresh ingredients, a statistician or data analyst needs high-quality data to cook up accurate predictions.

Example:

• A business might collect data on sales, ad spend, and customer demographics.
• A hospital could gather patient information like age, weight, and blood pressure.
• A sports analyst might use player stats like goals scored, minutes played, and passes completed.

👉 The better and more representative your data, the stronger your regression model will be.

2. Data Cleaning and Preprocessing: Preparing the Recipe

Raw data is messy. It may contain missing values, outliers, or inconsistencies. Preprocessing ensures the model doesn’t get “confused” by junk data.

Steps include:

• Handling Missing Values: Filling in or removing gaps (e.g., if age is missing for some customers).
• Removing Outliers: Extreme values that distort results (e.g., a house listed at $100 million in a middle-class neighborhood).
• Normalization/Scaling: Making sure variables are on a comparable scale (e.g., income in thousands vs. age in years).
• Encoding Categorical Variables: Turning words into numbers (e.g., “male/female” → 0/1).

👉 Think of this as cleaning the kitchen before cooking — messy ingredients ruin the dish.

3. Fitting the Model: Finding the Best Line

Once the data is ready, it’s time to fit the model — i.e., estimate the coefficients (slopes) that best describe the relationship between variables.

For a simple linear regression:

Y=a+bX+ϵ

The computer finds the values of a (intercept) and b (slope) that minimize the difference between predicted values and actual values. This is often done using a method called Ordinary Least Squares (OLS), which finds the “best-fit line.”

Example:

If we’re predicting sales from advertising:

Sales=500+20×(AdSpend)

It means: with no advertising, sales are $500, and each extra dollar spent on ads brings $20 more in sales.

4. Testing & Evaluation: Checking the Flavor

Like tasting your dish before serving, you need to test how good your model is. We typically split data into two sets:

• Training Data: Used to build the model.
• Testing Data: Used to check how well it performs on unseen data.

Key metrics include:

• R² (Coefficient of Determination): Tells us how much of the variance in Y is explained by X. (Closer to 1 = better).
• RMSE (Root Mean Squared Error): Measures prediction errors. Lower is better.
• Accuracy (for logistic regression): Percentage of correct yes/no predictions.

👉 A model that performs well on both training and testing data is reliable. One that performs well on training but poorly on testing suffers from overfitting (it memorized the data instead of learning the pattern).

5. Interpretation (Turning Numbers into Stories)

The final step is interpreting the results in plain language. This is where regression goes from math to meaning.

Example:

• In a health model: “Every 1 unit increase in BMI increases the risk of diabetes by 8%.”
• In a real estate model: “Each additional bedroom raises house price by $10,000.”
• In a marketing model: “Every $1,000 spent on social media ads boosts sales by 5%.”

Numbers alone don’t drive decisions. Stories do. Interpretation translates the equations into actionable insights that businesses, doctors, and policymakers can actually use.

Building a regression model is a structured journey: collect → clean → fit → test → interpret. When done right, it transforms raw data into a crystal ball one that doesn’t just explain the past, but also helps predict and shape the future.

Common Pitfalls and Misconceptions in Regression

Regression is powerful, but like any tool, it’s easy to misuse. A hammer can build a house or smash your thumb the same goes for regression models. Let’s explore some of the most common mistakes (with a few fun examples).

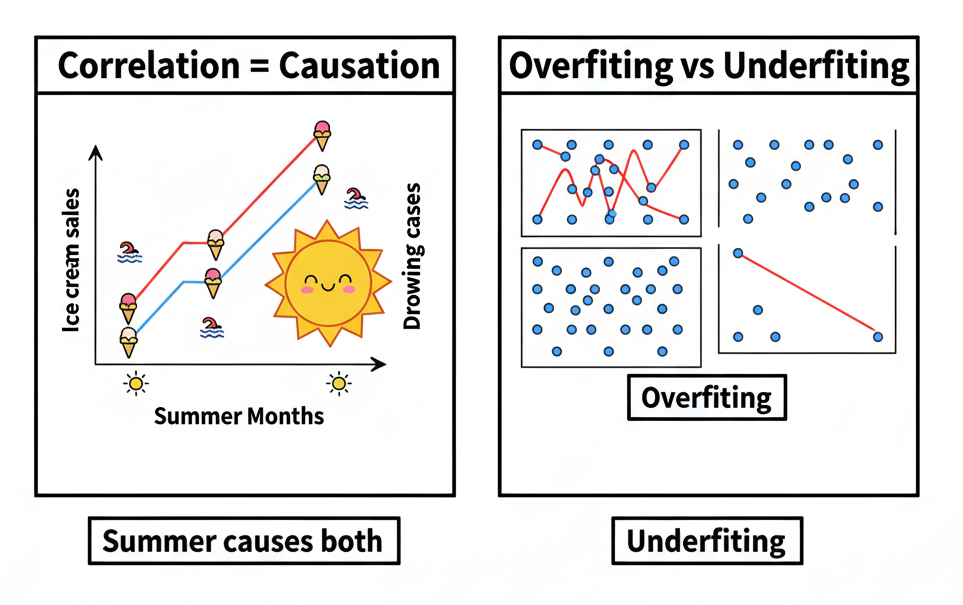
1. Correlation vs. Causation: The Oldest Trap

Just because two things move together doesn’t mean one causes the other.

Example:

• Ice cream sales and drowning incidents both increase in summer. Does eating ice cream cause drowning? Of course not it’s the hot weather driving both.

In regression, if we’re not careful, we might interpret strong correlations as causal links. But correlation only shows association, not cause and effect.

👉 Always ask: “Could there be a third factor influencing both variables?”

2. Overfitting & Underfitting (The Goldilocks Problem)

• Overfitting: The model learns the data too well, even memorizing random noise. It fits the training data very well but completely breaks down on unseen data. Imagine a student who memorizes every example in the textbook but can’t solve a slightly different problem in the exam.
• Underfitting: The model is too simple and fails to capture real patterns. Like using a straight line to describe a roller coaster.

Relatable Example:
Trying to predict fashion trends using only “year” as a variable? That’s underfitting. Adding every celebrity’s Instagram post into the model? That’s overfitting.

👉 The sweet spot is finding a balance: a model that’s complex enough to capture patterns, but simple enough to generalize.

3. Ignoring Assumptions: Blindfolded Driving

Regression comes with assumptions — like linearity, independence of errors, and homoscedasticity (equal variance of errors). Ignoring these is like driving blindfolded. Sure, you might move forward for a while, but a crash is inevitable.

Example:

If errors are not independent (like time-series stock data where yesterday’s errors affect today’s), standard regression results become misleading. That’s why we need specialized models like time-series regression.

👉 Rule of thumb: Always check assumptions before trusting results.

4. Funny/Relatable Mistakes

• Spurious Regression: A famous example showed a strong correlation between the number of Nicolas Cage movies released each year and swimming pool drownings. Funny? Yes. Useful? Absolutely not.
• Forgetting Units: Predicting someone’s salary in cents instead of dollars and proudly announcing they earn 2,000,000 — only to realize it’s $20,000.
• Ignoring Context: A model predicts people who buy more baby diapers also buy more beer. Does that mean diaper ads should be placed in liquor stores? Not necessarily — but it’s a real-world finding (new parents, anyone?).

Regression is like a sharp knife: powerful in the right hands, dangerous in the wrong ones. By remembering that correlation doesn’t always mean causation, avoiding over- or underfitting, and respecting the underlying assumptions, we can use regression as the precision tool it was meant to be instead of creating hilarious (and useless) statistical accidents.

The Future of Regression in AI & Machine Learning

Regression may seem like an old-school technique compared to modern deep learning buzzwords, but it’s far from obsolete. In fact, regression remains the foundation stone of artificial intelligence (AI) and machine learning (ML). Without it, today’s powerful algorithms wouldn’t exist.

Regression (The Quiet Engine Behind AI)

At its core, AI is about finding patterns in data and making predictions exactly what regression does. Before neural networks, decision trees, or gradient boosting, regression models were the workhorses of prediction. Even now, regression techniques are often the first step in building an ML pipeline, providing a baseline to compare more complex models against.

• Predicting house prices? Start with linear regression.
• Forecasting whether a customer will churn? Logistic regression often comes first.
• Estimating demand curves? Multiple regression is still a trusted tool.

👉 Think of regression as the “alphabet” of predictive modeling. Without learning the alphabet, you can’t write novels and without regression, you can’t build cutting edge AI.

Role in Deep Learning and Predictive Analytics

Even in the era of massive neural networks, regression lives on just in different clothes.

• Neural Networks: At the final output layer, most neural nets still use regression like functions. For example, predicting a continuous value (like stock price) is just linear regression inside a neural net. Logistic regression powers classification outputs (yes/no, cat/dog, spam/ham).
• Predictive Analytics: Businesses still rely on regression because it’s transparent and interpretable. While a deep learning model may give higher accuracy, regression can explain why a prediction is made which is critical in healthcare, finance, and law.
• Hybrid Models: Many modern algorithms combine regression with machine learning. For example, Elastic Net regression is widely used in high-dimensional genetics data, while regression trees blend with boosting methods for superior accuracy.

Future Outlook: Regression in the Age of AI

Looking forward, regression is unlikely to disappear. Instead, it will evolve as a trusted companion to AI:

• Explainable AI (XAI): As black-box models face criticism, regression’s simplicity and interpretability will make it more valuable.
• Big Data Applications: With data volumes exploding, scalable regression methods will help analysts extract insights without always relying on complex models.
• Automated Machine Learning (AutoML): Regression will remain a key part of AutoML pipelines, giving quick benchmarks before complex algorithms are deployed.

👉 In other words, regression is not competing with AI it’s fueling it, grounding it, and guiding it.

Regression may have been born in the 19th century, but it continues to drive 21st-century innovation. Whether embedded in a neural network, used in predictive dashboards, or serving as the explainer behind complex models, regression proves that sometimes the “old guard” isn’t outdated it’s timeless.

Conclusion (Turning Numbers Into Stories)

Imagine standing at a busy train station, trying to guess which train will arrive first. To the naked eye, it feels like chaos whistles, lights, people rushing everywhere. But with the right lens, you notice the schedule, the patterns, the rhythm. Suddenly, the chaos makes sense. That’s exactly what regression analysis does: it transforms overwhelming data into clear, actionable stories.

Throughout this journey, we’ve seen how regression predicts house prices, helps doctors diagnose patients, enables Netflix to recommend your next binge-worthy show, and even fuels the engines of artificial intelligence. What might look like just “math on paper” is actually a decision-making superpower one that turns uncertainty into insight.

The true beauty of regression isn’t just in its equations but in its ability to explain the world. It tells us not only what is happening, but also why and how. In a world drowning in data, regression models act like compasses, guiding businesses, governments, and individuals toward smarter choices.

So the next time you see a weather forecast, a product recommendation, or a stock prediction remember: behind the scenes, regression is quietly turning raw numbers into meaningful stories that shape our everyday lives.

FAQ’s